How to learn data modeling
If you want to turn your program idea into some reality, you need to model the data you will work with first. It doesn't matter how you are going to implement the system - the limitations are pretty similar, no matter if we:
- build classes in any programming languages out there
- design database for storing the data
- describe schemas for APIs
- put the data into some no-code/low-code solution - such as google sheet or airtable
We will have to organize our data into a logical structure that allows the use cases we want to support in all those cases.
How to learn data modeling then?
It's a practical skill, and you learn it best by doing. This article will walk you quickly through the challenges you face here and propose a simple exercise to get you started. You can even pick it as homework if you want:)
How to go about design
Start light. Pen and paper are the easiest or any application that allows you to sketch. You want to keep your form as light as possible - make circles, squares & arrows as you feel them fit. It should make sense to you, and in the given moment only - you are expected to recreate it as your understanding of the problem improves. Example of my design:
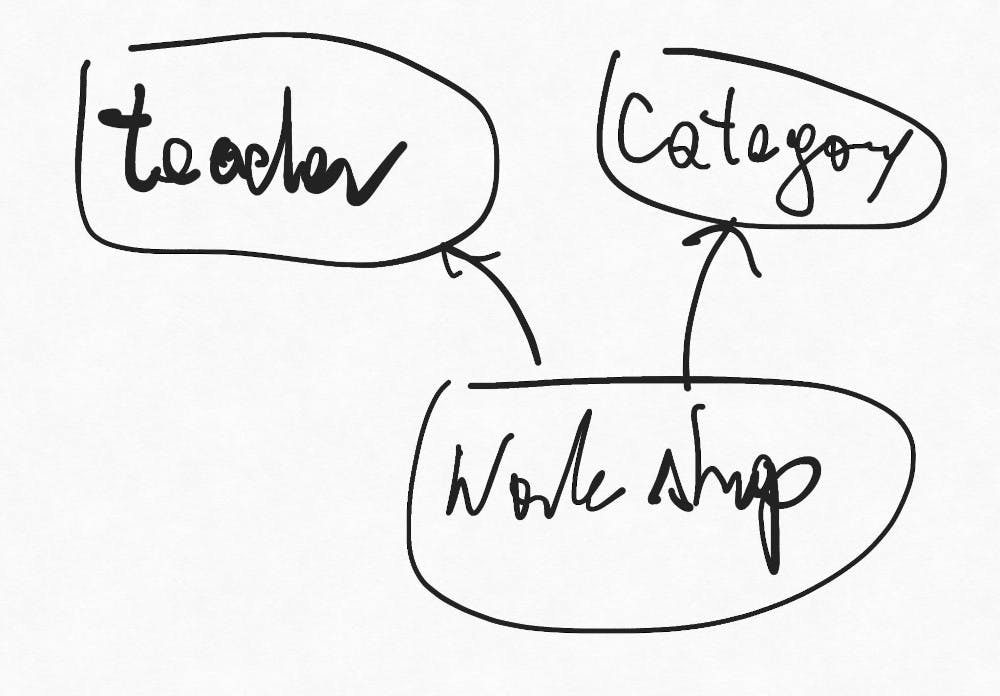
As you work on your example, you will get a better & better understanding - with each iteration having fewer changes. You can make your example more solid & move it to some text editor. At this stage, it looks like:

Categorize data types
Whatever your system is about, there will be some data types. In the case of a book shop, you can expect types such as:
- book
- author
And more, depending on what our system is supposed to do. If you want to suggest other books from the series or the genre - you will need to introduce those somewhere in your data model, probably as different types.
What value should we store for each type
Once you have the types, you must decide what values you store for each element in the system. Even for widespread types - users, clients, etc., you will have differences depending on what your application is supposed to do. For example, if you:
- invoice customers - you need their tax ID and billing address
- send them packages - you need their address
- offer birthday discount - that needs a birthday date
Deciding on those fields is the first step of customization of your application - it's only you who knows what uses-cases you have now, or consider adding later, so there is no guide you can follow & you have to figure out this on your own.
How to store values
The database could keep the same value in many ways:
- Name: First name & last name as separate values as above, but with a middle name or title added ** free text to keep them all
- Address free text, maybe multiline to allow for some organization separate fields, with various levels of precision - for example, the region could be free text or a list of available options based on the country. Road type - street/square /avenue/etc - can be included or skipped
- Birthday or any other date
date or date-time format that our tool provides
text, maybe with some validation - date-times often store more data than we need, it can make sense to keep
24-08for a birthday, instead of the whole date.
As you can see, there are plenty of options, and you need to think well through how you will use it, so you can avoid mistakes that will be difficult to solve later.
Common value types
Every system you will represent your model offers you a bit different values. Often you can see some variation of:
- free text - as much text as you can fit inside
- limited text - up to X characters
- numbers integers decimal - suitable for storing money values - it keeps its precision in the whole span of the values ** float - floating-point value, which is losing accuracy as you get further from 0. Ok for physics simulations, but problematic while dealing with money
Tricky value types
Thinks that varies between databases:
- files - often it's not possible, or not recommended to store files (for example, images) in the database directly. In those cases, you keep the file on some other sever & hold its location in the database
- nested values - if your customer object can have multiple addresses attached to it, it would be two tables with a one-to-many relationship in SQL or a nested array in no-SQL database
Class models typically support those values in some excellent way.
Think through your use cases
I make sense to spread this work a bit. Start with stretches one day, improve to a more precise form some other day, and review it or discuss with someone ever later. In this way, you will find whole in your design before spending much time on the implementation - what a great way of saving time!
Homework
If you have a project you want to start, you can follow the steps I describe above to design your data structure. You can share it here in the comments if you like! I'll definitively take a look at it.
The next stop will be to start implementing your design in any database or programming language you use. The implementation can be challenging, but definitively is easier when you know what you are building & why you need it all.
Let's get in touch
Are you interested in learning more about data modeling & AirTable? You can register here to get access for free to my course when it is ready:
Are you interested in discussing this or other topics covered on this blog? That's great; I'm always happy to talk with readers! You can add me a meeting here: calendly.com/marcin-wosinek/dev-meeting
Summary
I hope I have convinced you to give it a try to design your data structure. It's often tempting to either jump to programming without much thought or delay thinking about data structure when you know enough about the tools you use. Both approaches stop you from learning how to organize your data, which is a critical skill when you design a system of any kind.
